Le choux romanesco est l'archétype de la fractale-dans-la-vraie-vie (source)28 août 2022
Le choux romanesco est l'archétype de la fractale-dans-la-vraie-vie (source)
C'est en arpentant TikTok que je me suis pris d'un intérêt renouvelé pour les fractales. L'endroit est curieux, mais que voulez-vous, on y trouve de tout, et leur algorithme est si bon — à un point tel que c'en est inquiétant — qu'on finit toujours par tomber sur les niches correspondant à nos passions les plus tristes. J'étais sur TikTok donc, et une jeune femme entreprenait maladroitement de dessiner un triangle de Sierpiński en utilisant le jeu du chaos. Si les termes que je viens de citer vous échappent, nulle inquiétude, on va les prendre dans l'ordre.
Le triangle de Sierpiński est une figure usuellement obtenue comme suit :
Si vous répétez le processus suffisamment de fois (une infinité de fois en théorie, mais on risque de se heurter au mur de la réalité), vous allez aboutir à une figure nommée le triangle de Sierpiński :
Cette figure est une fractale, c'est à dire que si on agrandit une partie de la figure, on retrouve la figure entière. Par exemple ici, la moitié supérieure est une copie de la figure entière.
Si vous me permettez une incursion rapide dans les considérations mathématiques, cette propriété fait que les fractales n'appartiennent pas à une dimension entière, c'est-à-dire que ce ne sont ni complètement des lignes, ni des surfaces, ni des volumes. Elles ne sont pas exactement de dimension 1, 2 ou 3. Pour calculer leur dimension exacte, on peut faire l'analogie avec les figures classiques : si on multiplie la taille d'un cube par deux, son volume est multipliée par huit, soit deux à la puissance trois, car un cube est en dimension 3.
Pour trouver la dimension d'un triangle de Sierpiński, on peut noter que si on multiplie sa taille par deux, alors sa « surface » est multipliée par 3. Ainsi, sa dimension est égale à log(3)/log(2), soit environ 1,585. Le triangle de Sierpiński est donc environ à mi-chemin entre la ligne et la surface. Pour plus d'informations, voyez le concept de dimension de Hausdorff. Fin des calculs, retour à l'article.
Pour revenir à TikTok, je disais donc que la jeune femme avait opté pour une autre méthode, le jeu du chaos. Le processus est différent :
Ce processus a l'intérêt d'être assez ludique, aussi ai-je pris l'initiative de coder un script pour en simuler le fonctionnement. Rien de bien ambitieux pour l'heure, quelques lignes de Python qui génèrent une image au format SVG. Ce format texte a le bon goût d'être très facile à manipuler et se prête très bien aux images très géométriques avec lignes, points et polygones. Voyez comme c'est simple :
.jpg){kind=link}
<svg viewBox="0 0 1000 1000">
<rect width="100%" height="100%" fill="white"></rect>
<circle cx="66.98729810778065" cy="749.9999999999999" r="5"></circle>
<circle cx="933.0127018922192" cy="750.0000000000002" r="5"></circle>
<circle cx="500.00000000000034" cy="1.1368683772161603e-13" r="5"></circle>
<circle cx="487.55600750513696" cy="767.3399306075027" r="2" fill="red"></circle>
<circle cx="710.284354698678" cy="758.6699653037515" r="2"></circle>
<circle cx="388.6358264032293" cy="754.3349826518756" r="2"></circle>
<circle cx="660.8242641477243" cy="752.1674913259379" r="2"></circle>
<circle cx="796.9184830199717" cy="751.083745662969" r="2"></circle>
...
</svg>
Voici donc un triangle de Sierpiński produit avec cette méthode :
Cette figure comporte 50 000 points. On voit qu'on retrouve avec une précision surprenante le motif que nous avons déjà vu plus haut. À droite du sommet, on peut voir le premier point placé marqué en rouge, ainsi que sur le côté droit en dehors du triangle les points placés après, avant que le tracé ne vienne à l'intérieur du polygone pour ne plus en sortir.
Avec cet outil entre les mains, les multiples possibilités commencent à nous apparaître. En premier lieu, que se passe-t-il avec un autre polygone ? Ni une, ni deux, testons avec un carré. Ma déception fut perceptible.
C'est un carré du chaos.
Avec un carré, la répartition est donc parfaitement aléatoire. La science avance. En relisant l'article de Wikipédia en anglais sur le jeu du chaos, il est effectivement mentionné que « If the chaos game is run with a square, no fractal appears and the interior of the square fills evenly with points. However, if restrictions are placed on the choice of vertices, fractals will appear in the square ».
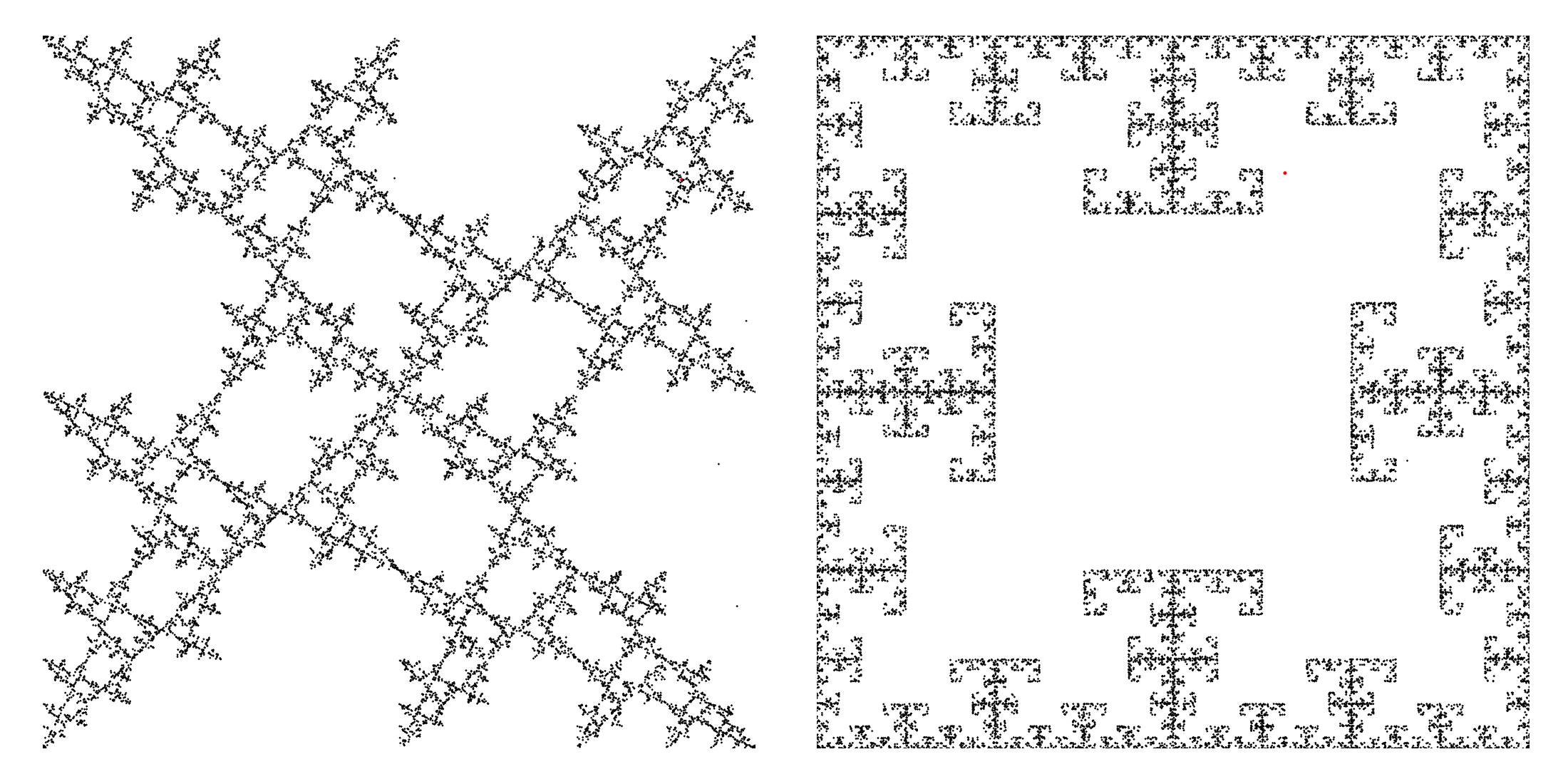
Par exemple, si dans notre carré on ne choisit pas à chaque tour parmi tous les sommets au hasard, mais on exclut du tirage au sort le sommet déjà choisi au tour précédent, on obtient la figure suivante, à l'esthétique bien plus intéressantes :
Il ne s'agit pas de la seule contrainte qu'on peut imposer dans la sélection du sommet. En fait, si à chaque tour on numérote les sommets dans le sens horaire à partir de zéro, zéro étant le sommet choisi au tour précédent, on peut coder une restriction en indiquant la liste des nombres parmi lesquels on peut choisir le prochain sommet. Ainsi, dans un carré, il y a quatorze « restrictions » possibles : (0) ; (0,1) ; (0,1,2) ; (0,1,2,3) ; (0,2) ; (0,2,3) ; (0,3) ; (1) ; (1,2) ; (1,2,3) ; (1,3) ; (2) ; (2,3) ; (3).
Dans cette liste, (0,1,2,3) et (1,2,3) sont les deux versions illustrées juste au-dessus. En effet, (0,1,2,3) correspond à l'ensemble des sommets du carré et dans (1,2,3) on a retiré le « 0 » correspondant par définition au sommet choisi au tour précédent. Si on essaie les versions (0,1,2) et (0,1,3), on a les résultats suivants :
C'est quand même plus rigolo que les nuages de points
On constate donc qu'on peut jouer sur deux facteurs : le nombre de côtés du polygone de départ et les contraintes sur le choix du sommet. Ces deux paramètres permettent la génération d'un grand nombre de figures variées, dont la plupart sont au moins aussi intéressantes que le triangle de Sierpiński d'où nous avons commencé notre voyage.
Si on s'intéresse aux pentagones, c'est encore un autre univers :
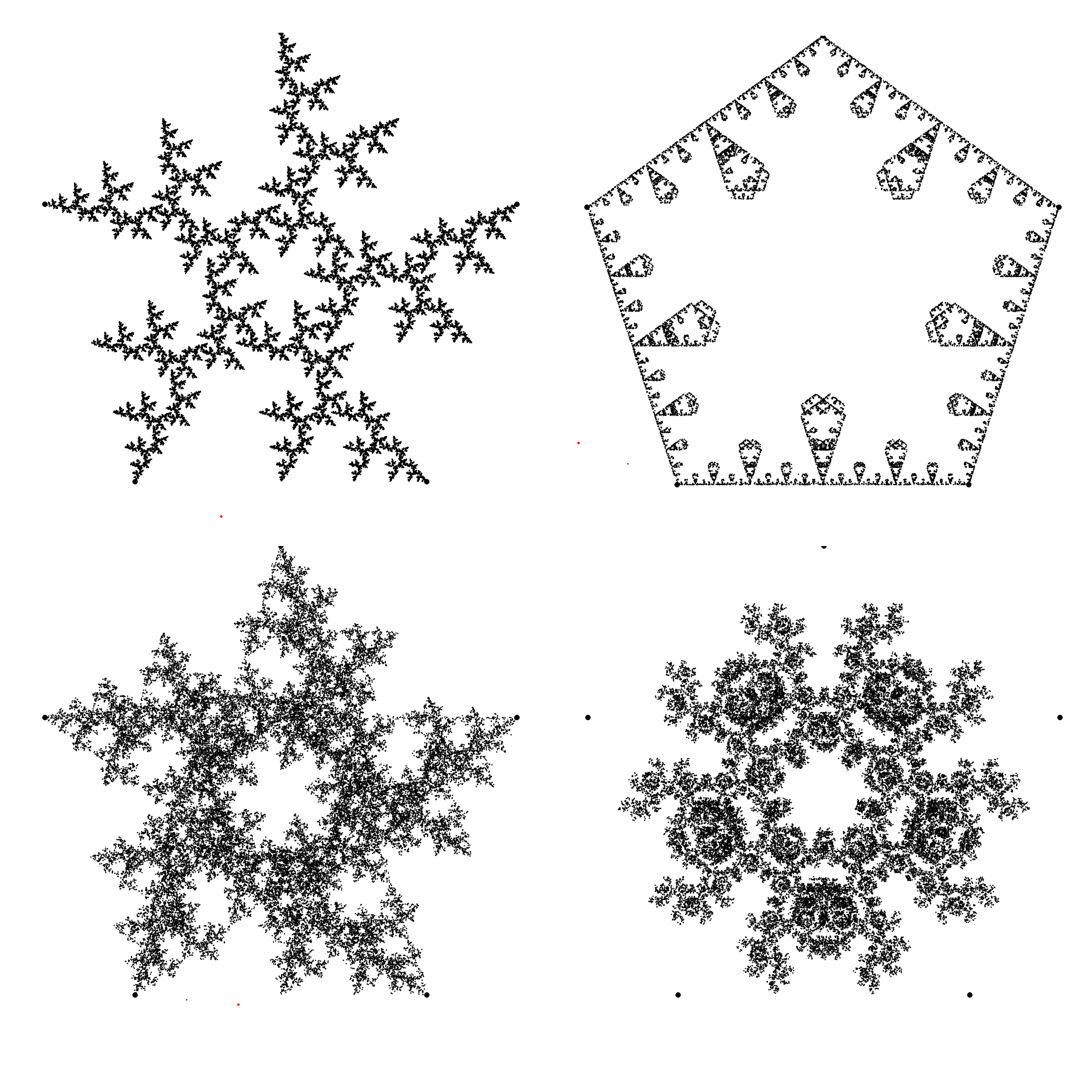Dans le sens de la lecture, nous avons (0,1,2) ; (0,1,4) ; (0,1,2,3) et (1,2,3,4), avec 50 000 points à chaque fois
En cherchant de nouvelles figures et avec ces nouvelles contraintes, le petit script Python du départ s'est avéré limité. Désireux d'avoir un outil pratique pour faire mumuse avec les jolis dessins, je me suis attelé à la conception d'une page web permettant de générer facilement les images. Le cahier des charges était de pouvoir renseigner un nombre de côtés, un nombre de points, une sélection de sommets, et d'en sortir une figure.
La transposition du Python au Javascript est aisée, mais je dois maintenant gérer un nombre quelconque de côtés. Pour trouver les coordonnées des sommets du polygone régulier, je ressors mes vieux souvenirs de classe préparatoire et les racines énièmes de l'unité. Un passage par le plan complexe plus tard, on trouve que si \(x_{0}\) et \(y_{0}\) sont les coordonées d'un sommet et \(n\) est le nombre de côtés du polygone, alors les coordonnées des sommets suivants seront :
$$x_{k+1} = x_{k}\cos\left(\frac{2\pi}{n}\right) - y_{k}\sin\left({\frac{2\pi}{n}}\right)$$
$$y_{k+1} = x_{k}\sin\left(\frac{2\pi}{n}\right) + y_{k}\cos\left({\frac{2\pi}{n}}\right)$$
La génération de l'image au format SVG ne pose pas plus de problème. Le défaut du SVG cependant est qu'il s'intègre tant à la page web qu'il est difficile de l'en sortir et de télécharger l'image produite. On ne peut pas en tout cas faire bêtement clic droit, « Enregistrer l'image sous… ». Je me suis donc lancé dans la tâche ardue de convertir le SVG en PNG, avant de reculer devant la tâche. J'ai fait un pas de côté pour générer un canvas. C'était finalement encore plus simple à manipuler que le SVG, et la conversion en PNG était facilitée.
Au bout du compte, vous pouvez à votre tour générer des images selon le jeu du chaos sur cette page. Le bagage scientifique me manque pour que je m'avance à qualifier de fractales toutes les images obtenues, on peut néanmoins au moins apprécier l'esthétisme graphique que nous offrent les mathématiques.
Panel de figures. Dans l'ordre de la lecture : heptagones (0,1,2) ; (0,1,3) ; (0,1,4) ; (0,1,5) ; (0,1,6) et hexagones (1,4,5) ; (2,4,5) ; (3,4,5)
Merci d'avoir lu jusqu'ici. Pour récompenser votre patience, voici la jeune femme de TikTok que j'évoquais plus tôt qui réussit enfin à tracer son triangle après avoir acquis une règle.