(c) Freepik28 octobre 2025
Il m’arrive par moment de me piquer d’intérêt pour les vidéos de voyage et « d’aventure » sur YouTube (l’aventure pouvant parfois se résumer à une promenade en nature). Un thème récurrent dans les médias de ce genre est le choix d’un point au hasard avec l’objectif de s’y rendre, voire d’en revenir (exemple 1, exemple 2).
L’algorithme de choix n’est généralement pas excessivement détaillé, ou alors se résume en un choix dans un rectangle compris entre deux méridiens et deux parallèles, ce qui n’est pas très enthousiasmant comme problème à résoudre. En effet, il suffit dans un rectangle de choisir une abscisse et une ordonnée entre les deux bornes limites. Mon tropisme naturel et mon esprit franco-centré m’a donc naturellement conduit à me poser la question la plus naturelle : comment ferait-on pour choisir un point au hasard en France ?
Un premier instinct serait de délimiter la France dans un rectangle (ou plusieurs rectangle) et de croiser les doigts pour ne pas tomber dans l’eau ou un pays limitrophe. Ou alors recommencer jusqu’à ce qu’on tombe juste. Mais ce n’est pas très élégant et encore faudrait-il être capable de déterminer algorithmiquement si un point est bien sur le territoire français. Et pour cela, il va nous falloir quelques données.
Je me suis d’abord lancé à la recherche d’une liste des points frontaliers de la France. Je pensais naïvement que je trouverais ça avec l’API d’Etalab geo.api.gouv.fr, qui fournit déjà le tracé des communes, départements et régions, mais en fait non. Je me suis ensuite tourné vers l’IGN, mais chou blanc également. C’est donc sur OpenStreetMap que j’ai fini par trouver mon bonheur, mais ça n’a pas été une sinécure. Alors que je pensais m’en tirer avec un bête clic droit « Télécharger la frontière », c’est sur l’obscur overpass-turbo.eu que j’ai fini par trouver mon bonheur, avec cette requête que je ne saurai plus vous expliquer, probablement tirée de la lecture croisée de trois forums différents.
[out:json][timeout:25]
relation(16467322);
(._;>;);
out body;
J’en ai donc tiré un fichier GeoJSON contenant une liste de près de 2 000 polygones formant la France métropolitaine, les plus grands constituant la France continentale (380 365 côtés), puis la Corse (79 359 côtés) et Ouessant (16 678 côtés). Autant dire qu’on suit le tracé de la frontière d’assez près.
Paradoxe du littoral, illustration.
Maintenant qu’on a ces informations, la réflexion peut commencer. Le prochain défi est de passer de la représentation géographique à la représentation géométrique. Tous ces points doivent être placés sur une carte. Pour cela, le choix d’une méthode de projection s’impose. Après quelques recherches, la projection conique conforme de Lambert paraît être le système de référence en France métropolitaine (il y a même un décret dessus, c’est dire si c’est sérieux). Son principal défaut cependant est d’être parfaitement imbuvable et d’une complexité bien supérieure à l’ambition initiale du projet et à mes propres compétences en la matière.
J’ai donc opté pour une méthode plus simple à mettre en œuvre, en l’espèce la projection sinusoïdale : l’ordonnée d’un point est proportionnelle à sa latitude, et l’abscisse est ajustée proportionnellement à la longitude et au cosinus de la latitude (si vous me permettez un excès d’arrogance, j’ai redécouvert la méthode par moi-même avant de découvrir qu’elle avait déjà un nom). L’enjeu est d’assurer une représentation à peu près réaliste des surfaces. Sinon, en assimilant longitude et latitude à abscisse et ordonnée comme dans la projection de Mercator, on représente le nord de façon disproportionnée par rapport au sud et le tirage aléatoire d’un point n’est plus uniforme sur le territoire. Dans le détail, on pose les variables suivantes :
Puis on définit pour notre convenance la variable \(r\) suivante :
On peut enfin faire nos calculs, avec \(x\) le numéro de colonne du pixel correspondant au point sur l’image et \(y\) le numéro de ligne :
$$x = M+\frac{L}{2}+r\cdot\left(\lambda-\frac{\lambda_{max}-\lambda_{min}}{2}\right) \cdot \cos \left(\phi\right)$$
$$y = M+r\cdot\left(\phi_{max}-\phi\right)$$
Après des calculs dûment réalisés on obtient la représentation suivante, ma foi pas honteuse :
Hum, oui, c’est la France quoi
Une note : pour placer les points sur l’image on prend des valeurs entières de \(x\) et \(y\), mais pour la précision des calculs on conserve les valeurs flottantes (avec des chiffres après la virgule).
L’enjeu à présent est de réussir à choisir un point au hasard dans un de nos polygones de façon uniforme. Pour cela on ne va pas utiliser la méthode évoquée plus haut du point tiré dans un rectangle jusqu’à tomber sur le territoire. On va partir sur un autre procédé plus satisfaisant (à mon sens, vous savez, les goûts et les couleurs). En l’espèce, les polygones ont le bon goût de tous pouvoir être découpés en triangles et l’algorithme pour choisir un point au hasard dans un triangle est simple à mettre en œuvre. Prochaine étape donc : la triangulation du territoire (hommage aux Cassini). Pour cela, j’ai repris le code de ce dépôt sur GitHub, qui a bien fait le travail.
Enfin bon, il a bien fait le travail mais il a quand même pris son temps, le bougre. 30 heures. Je veux bien croire que mon PC n’est pas une bête de course mais soyons sérieux.
Deux dodos plus tard, donc, j’avais à disposition une liste d’environ 600 000 triangles (pour à peu près autant de points dans mon fichier d’origine). Le plus petit est de l’ordre de \(10^{-15}\) pixels (vous n’aviez sûrement encore jamais vu de femto-pixels auparavant) du côté de l’Île d’Yeu ; le plus grand est de l’ordre de 1,3 million de pixels ; et la surface totale couverte est d’environ 5,1 millions de pixels. Pour le plaisir de vos yeux voici à quoi ressemble la triangulation sur la carte.
La France est divisée.
Le calcul de l’aire de chaque triangle permet de choisir un triangle au hasard en pondérant selon la surface : il faut en effet qu’on ait un peu plus de chance de tomber sur notre gros triangle qui occupe un quart de la surface du pays que sur notre micro-machin dans l’Atlantique. Notez que je parle ici de surfaces mesurées en pixels mais l’idée est d’avoir des valeurs proportionnelles aux vraies aires. Les superficies inférieures à un pixel sont théoriques, d’une part car invisibles sur la carte, et d’autre part leur probabilité d’être choisie est négligeable. Je les ai tout de même inclues dans mes petits calculs par soucis de complétude.
Pour choisir un triangle au hasard, on classe nos triangles par ordre de taille, du plus petit au plus grand, et on crée à côté une liste des surfaces cumulées de nos triangles : la première valeur est égale à la surface du premier triangle, la deuxième à la somme des surfaces des deux premiers triangles, la troisième des trois premiers… puis la dernière valeur de la liste est la surface totale des triangles. Il ne nous reste plus qu’à choisir un nombre au hasard entre 0 et la surface totale, et on remonte la liste des surfaces cumulées jusqu’à dépasser la valeur tirée. Notre position dans la liste indique le triangle retenu.
Pour choisir un point au hasard dans le triangle, j’ai adapté la méthode proposée ici sur Stackoverflow par un aimable contributeur.
Pour la mise en œuvre pratique de ces considérations algorithmiques, j’ai fini par mettre de côté Python. En effet, les scripts dans le terminal, c’est rigolo mais ce n’est pas très visuel et c’est difficile d’accès. J’ai donc entrepris le développement d’une page web dédiée pour la démonstration (eh oui, vous pourrez jouer à la fin de l’article, tout ceci n’est pas purement théorique). L’objectif est d’avoir un gros bouton qui affiche un point sur la carte et les coordonnées géographiques correspondantes.
En synthèse, j’affiche sur la page ma carte que je vous ai montré au début et je superpose par dessus un objet <canvas>. Quand je clique sur un bouton, les opérations que je vous ai décrites juste avant se réalisent : choix d’un triangle et choix d’un point dans le triangle. Il n’y a plus qu’à faire les opérations pour la projection que je vous ai décrites précédemment en sens inverse. Pour placer le point sur la carte, il faut prendre en compte le redimensionnement de l’image mais rien de plus compliqué qu’une règle de trois.
Je vous passerai mes prises de tête avec Javascript et le CSS pour que tout soit aligné comme il faut, mais j’ai tout de même rencontré un petit souci pratique qui vaut bien un détour : la liste des triangles occupe relativement beaucoup de place (75 Mo) et la page prend bien dix secondes à se charger (sur mon ordinateur encore une fois, ce n’est pas une référence absolue mais ça incite à se poser des questions d’optimisation). Plutôt que de charger les triangles avec une balise <script> j’ai donc opté pour une solution alternative où tous mes triangles sont répartis dans autant de fichiers (près de 600 000 donc). Une fois que je connais l’index du triangle dans lequel je vais faire la suite de mes opérations, je l’appelle unitairement dynamiquement (les fichiers s’appellent 0, 1, 2... 599591 et font quelques octets chacun) pour un « coût » minime (si ce n’est l’enfer de gérer de l’asynchrone et les promesses Javascript).
Le site est statique et fonctionne complètement en local. Si vous voulez récupérer le code, vous pouvez faire Ctrl+U. Il faudra aussi penser à récupérer tout le contenu du dossier script/triangles/.
Évidemment, alors que j’écris ces lignes, j’ai entamé la copie des fichiers vers le serveur et je commence à remettre en question la pertinence de mes choix parce que 600 000 fichiers de 100 octets prennent bien plus de temps à la copie qu’un seul faisant la même taille cumulée. Tous ces femto-pixels valaient-ils vraiment la peine d’être pris en considération ?
Trève de plaisanterie, vous pouvez vous amuser dès maintenant en cliquant juste en dessous.
Je ne suis toujours pas web designer.
J’ai hésité à finasser avec des fonctionnalités supplémentaires, pour pouvoir choisir le territoire sur lequel on veut tirer notre point au hasard (commune, département, région, outre-mer compris), un historique des points tirés avec possibilité de conserver les points sur la carte au fur et à mesure, un cookie pour retrouver son historique quand on retourne sur la page, un appel API pour afficher la commune d’atterrissage… Bref, les idées ne manquaient pas, mais il faut aussi savoir se satisfaire d’un produit qui fonctionne. Je laisse quand même cette road map ici si la motivation me revient.
Pour ce qui me concerne, je ne suis pas encore parti à l’aventure. Ça viendra peut-être. J’avoue que je me suis lancé tête baissée dans le développement de ce machin en étant plus séduit par l’exercice intellectuelle que par un besoin réelle. Mais maintenant que c’est fait, charge à vous de vous en saisir, moi j’ai fait ma part du travail.
Merci pour votre attention.
4 février 2025
Le 21 décembre 2024, a été publiée au Journal officiel la fameuse loi spéciale qui doit permettre de pallier l'absence temporaire de budget pour l'année 2025. Le fond de la loi nous intéresse ici fort peu, mais un petit détail m'a interpelé dans le bas de la page.
La loi n'a pas été promulguée à Paris mais à Mamoudzou, la capitale de Mayotte. En effet, quand la loi a été promulguée le 20 décembre 2024, le chef de l'État était en déplacement sur l'île, sinistrée quelques jours auparavant par un cyclone.
Cela m'a conduit à me poser une question essentielle : Est-ce que cela arrive régulièrement ? Et quels autres lieux ont eu l'honneur d'être le théâtre d'une promulgation présidentielle ?
Pour y répondre, nous nous tournons vers Légifrance, « le service public de la diffusion du droit ». Bénie soit notre République moderne et numérique, une API nous est gracieusement mise à disposition afin d'interroger les fonds légaux.
L'API est un peu bordélique et ce n'est pas évident de s'y retrouver parmi toutes les commandes proposées pour consulter, rechercher, lister parmi les textes publiées, les textes consolidés ou les débats parlementaires. Mais, apprécions tout de même le fait qu'elle existe.
Cela nous permet donc d'interroger en particulier la base des Journaux officiels et d'y rechercher les textes publiés répondant à certains critères. En l'espèce, on ne recherche que les promulgations de loi. Les textes ne sont correctement enregistrés au format « texte » qu'à partir de 1990 (ce qui est déjà admirable en soi), pour les textes plus anciens on n'a souvent que le journal papier numérisé.
L'API renvoie des données JSON contenant les métadonnées des textes et leur contenu au format HTML. Les métadonnées incluent une variables signers, correspondant au bloc des signatures du texte. Il faut alors en extraire la chaîne de caractères "Fait " pour en tirer derrière le lieu de la signature (« Fait à Paris », « Fait à Mamoudzou »…).
Petite contrariété, certains textes gèrent mal cette donnée et le bloc de signatures est à aller chercher directement dans le corps du texte, à la fin du dernier article de la loi. Il faut alors naviguer péniblement dans les sections et sous-sections du texte jusqu'à trouver la dernière (non, elles ne sont pas toujours rangées dans l'ordre).
Ces obstacles surmontés, que disent les chiffres ? Après un peu de nettoyage et une petite revue manuelle, j'ai identifié depuis 1990, sur 3032 textes analysés pour lesquels le lieu de signature est indiqué, 99 textes promulgués hors de Paris :
| Lieux | Occurences |
|---|---|
| Paris | 2933 |
| Fort de Brégançon | 58 |
| Le Lavandou | 13 |
| Saint-Paul | 7 |
| Itacaré | 5 |
| Eugénie-les-Bains | 3 |
| Nouméa | 3 |
| Lyon | 2 |
| Port-Vila | 1 |
| Washington | 1 |
| Rio de Janeiro | 1 |
| New Delhi | 1 |
| La Mongie | 1 |
| Mamoudzou | 1 |
| Toulon | 1 |
| Charleville-Mézières | 1 |
En dehors de Paris (environ 97 % des textes), les lieux de villégiature des Présidents de la République se détachent. Il y a évidemment le Fort de Brégançon et Le Lavandou (pour rappel, Nicolas Sarkozy séjourna régulièrement au Lavandou où la famille de Carla Bruni possède une villa), mais aussi :
Les autres villes relèvent de déplacements plus classiques. Peut-être s'étonnera-t-on de l'absence de Versailles, où se trouve une autre résidence présidentielle et où Emmanuel Macron a passé du temps à l'isolement à la fin de 2020.
Par ailleurs, si on compte, pour chaque président, le nombre de promulgations délocalisées hors de Paris, on constate une tendance marquée.
| Présidents de la République | Promulgations hors de Paris |
|---|---|
| François Mitterrand* | 0 |
| Jacques Chirac | 14 |
| Nicolas Sarkozy | 18 |
| François Hollande | 4 |
| Emmanuel Macron | 63 |
* De 1990 à 1995 uniquement.
Il y a eu sous Emmanuel Macron une explosion des lois promulguées hors de Paris. Sur 99 textes promulgués hors de Paris depuis 1990, 63 l'ont étés sous sa présidence ! Alors qu'on pensait avoir fait le tour des anomalies statistiques le concernant, en voici une nouvelle qui vous est offerte sur un plateau. Cela peut s'expliquer par une forte activité en été, avec de nombreuses lois promulguées depuis le Fort de Brégançon : 1 à l'été 2018, 15 en 2019, 5 en 2020, 11 en 2021, 8 en 2022, 13 en 2023. Et aucun en 2024, trêve olympique oblige :o)
Dans le cadre de cette étude, je n'ai pris en compte que les lois (ordinaires, organiques et constitutionnelles) parce que le lieu de signature y est (presque) toujours renseigné ; ce n'est pas le cas pour les textes réglementaires où seule la date est (généralement) renseignée, quand les champs ne sont pas tristement laissées vides, comme un formulaire administratif un peu pénible.
1er octobre 2024
Autoportrait, par Joseph Ducreux
Ce blog renaît ! Après avoir longtemps procrastiné la refonte de ce site, je me suis enfin décidé à donner le coup de collier nécessaire pour y arriver.
Deux changements notables :
Sur ce dernier point, vous vous demandez probablement (toi le lecteur égaré) pour quelle alternative j'ai optée. Eh bien après avoir envisagé d'utiliser Hugo, qui n'avait finalement pas l'air plus simple d'usage, j'ai fini par me retrousser les manches pour pondre un script Python complètement de mon cru. Cela me permet de reprendre complètement la main sur la chaîne éditoriale et de m'abstraire des outils tiers dont je n'ai besoin finalement que d'une infime partie des fonctionnalités.
Je continue de rédiger mes articles en Markdown (je voulais quand même pouvoir reprendre mes anciens fichiers sources sans trop d'efforts), et mon script vient construire les pages une à une, sur la base d'une poignée de fichiers HTML « modèles », et les placer dans une arborescence de fichiers que je n'ai plus qu'à coller dans la destination. Le script n'a qu'une seule dépendance externe : le paquet PIP Markdown pour la conversion de Markdown vers HTML. J'ai brièvement hésité à recoder cette bibliothèque pour m'isoler complètement des contingences extérieures mais ça aurait été un effort disproportionné.
J'ai bien conscience que ce mode de fonctionnement me place très à contre-courant, à cette époque où Javascript est la nouvelle lingua franca, mais avoir un blog est une forme de contre-culture en soi. Ceci est donc une forme de démarche politique.
Je caresse le doux rêve que cela me permettra de bloguer plus facilement à l'avenir, sans prise de tête, éventuellement pour des articles plus courts mais plus fréquents, mais je ne me fais plus aucune illusion et je ne promets rien. Mais ce serait bien.
1er mai 2023
Logo du France Cybersecurity Challenge
J'ai pris part cette année au France CyberSecurity Challenge (FCSC dans le jargon), un challenge de cybersécurité organisé par l'ANSSI. Il consiste en plusieurs problèmes à résoudre, faisant appel à des connaissances dans des domaines variés comme la cryptographie, l'exploitation de binaires ou le web. Chaque problème rapporte un certain nombre de points, selon la difficulté.
Pour résoudre un problème, il faut trouver le flag (« sémaphore », en bon français) associé à ce problème, qui prend la forme d'une chaîne de caractère du type FCSC{br@v0_pour_1a_s0lu7ion}.
Je vais revenir ici quelques un des problèmes de cette édition que j'ai trouvé intéressant, ou à tout le moins que j'ai apprécié résoudre.
Pour faire patienter le public avant l'ouverture des épreuves, un problème de teasing était caché sur le site web, rapportant un avantage considérable de 1 point et le privilège de pouvoir afficher un Emoji 🔥 à côté du pseudonyme de ceux qui en viennent à bout.
La porte d'entrée n'était pas très difficile à trouver, elle était indiquée dans un commentaire du code source de la page d'accueil.
<p>
<!-- En attendant l'ouverture, un flag est à trouver sur ce site. Voir sur /teasing 🔥 -->
</p>
Sur la page indiquée (https://france-cybersecurity-challenge.fr/teasing donc), on trouve une image :
Cette image a visiblement été découpée et réagencée. Rien de mieux à faire dans l'immédiat que de la remettre dans l'ordre. Je me suis aidé d'un code Python pour recréer l'image, mais le puzzle a quand même été résolu à la main.
LSB = Least significant bit (« bit de poids faible »). La stéganographie, c'est le fait de dissimuler des choses dans un fichier, en particulier une image. « LSB Stegano » c'est donc une indication sur l'étape d'après. Dans une image, la couleur de chaque pixel est codée sur trois octets, chaque octet donnant la quantité de rouge, de vert et de bleu sur une échelle de 0 à 255.
Si on ajoute ou retire 1 à un octet, la différence est invisible à l'œil nu. Dès lors, on peut utiliser cette propriété pour dissimuler un message dans le dernier bit de chaque octet. Si on applique cette théorie à l'image que nous avons obtenue en prenant successivement le dernier bit de chaque octet dans chaque pixel, on obtient… une autre image.
Rebelotte :
Et cette fois-ci, si on prend encore le dernier bit de chaque octet de chaque pixel, on obtient un fichier binaire qui ne semble pas être une image cette fois ci.
$ file sortie.bin
sortie.bin: ELF 64-bit LSB pie executable, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, BuildID[sha1]=8633214f4900c48d504eb171c5013837f19a7d85, for GNU/Linux 3.2.0, stripped
On a donc un fichier exécutable. Dans le doute, on exécute.
$ ./sortie.bin
Il ne se passe rien. Le programme semble attendre quelque chose sur l'entrée standard. Et si on écrit quelque chose ?
$ ./sortie.bin
aaa
$
Le programme s'arrête. Bon. On suppose qu'il faut écrire quelque chose de précis pour obtenir un résultat intéressant. À ce stade j'étais un peu démuni parce que mes capacités dans cette discipline, la rétro-ingénierie, sont assez limitées. Après avoir un peu pataugé à essayé de lire du code assembleur, je me suis penché sur des outils de décompilation, qui visent à fournir un code en langage C équivalent à un exécutable donné. Après quelques soirées perdues à regarder des tutoriels sur YouTube et à me battre avec Ghidra, un logiciel de la NSA spécialisé dans ce type de tâches, j'ai fini par comprendre que le programme attendait en entrée le chemin pour sortir d'un labyrinthe.
j = 0;
i = 0;
ok = 1;
__isoc99_scanf("%188s",input);
raw_length = strlen(input);
length = (int)raw_length;
for (x = 0; x < length; x = x + 1) {
if (input[x] == 'L') {
i = i + -1;
}
else if (input[x] == 'R') {
i = i + 1;
}
else if (input[x] == 'U') {
j = j + -1;
}
else if (input[x] == 'D') {
j = j + 1;
}
if (*(char *)((long)maze + (long)i + (long)j * 64) == '#') {
ok = 0;
}
if (j < 0) {
ok = 0;
}
if (i < 0) {
ok = 0;
}
if (62 < j) {
ok = 0;
}
if (62 < i) {
ok = 0;
}
}
if (((ok == 1) && (j == 62)) && (i == 62)) {
puts("Congrats!! You can use the flag given by this command to validate the challenge:");
printf("echo -n %s | sha256sum | awk \'{ print \"FCSC{\" $1 \"}\" }\'\n",input);
}
Ci-dessus, un extrait du code obtenu. Dites-vous bien que j'ai renommé les variables pour faciliter la lecture parce qu'avant on avait du « local_1008 », du « puVar2 » ou du « sVar1 ». Aussi, si j'avais perçu assez vite l'histoire du labyrinthe à résoudre (l'emploi des lettres L, R, U et D est assez parlant), c'est la disposition du labyrinthe qui m'a causé le plus de soucis. En effet, ce dernier était encodé sous la forme d'un tableau dont Ghidra n'a pas jugé utile de me donner les valeurs, me renvoyant à la lecture du code d'assemblage. En outre, le C est un langage exigeant et quand on a l'habitude du Python il n'est pas évident de distinguer ce qui relève de l'addition innocente de ce qui relève de l'accès à un index dans un tableau.
J'ai tout de même fini par extraire l'allure du labyrinthe, et dès lors coder un algorithme de résolution était comparativement assez facile. Le chemin final consiste en 188 mouvements, décrits par L, R, U et D (respectivement, gauche, droite, haut et bas). Finalement :
$ ./sortie.bin
RDDD … RRRD
Congrats!! You can use the flag given by this command to validate the challenge:
echo -n RDDD … RRRD | sha256sum | awk '{ print "FCSC{" $1 "}" }'
$ echo -n RDDD … RRRD | sha256sum | awk '{ print "FCSC{" $1 "}" }'
FCSC{5cf9940286533f76743984b95c8edede9dbfde6226de012b8fe84e15f2d35e83}
Dans ce problème, on nous donne 79 images numérotées représentant chacune une carte perforée nous rappelant les premiers temps de l'informatique.
Une des images
L'énoncé du problème évoque « IBM029 » et précise « Sur les 79 cartes seules les 53 premières sont correctement numérotées, les dernières étaient dans une boîte qui a souffert du temps et a effacé les étiquettes collées dessus. ». Une recherche rapide permet de déterminer comment interpréter les cartes. Chaque carte comporte 12 lignes et 80 colonnes. Chaque colonne sur une carte correspond à un caractère, et les lignes sur lesquelles on trouve un trou renseignent sur le caractère encodé.
Par exemple, s'il y a un trou uniquement sur la troisième ligne, alors c'est le caractère 0 (zéro). S'il y a un trou sur les deuxième, septième et onzième lignes, alors c'est le caractère * (astérisque). On en titre que l'image donnée en exemple doit être interprétée ainsi :
INTEGER :: S1(256) = (/ 96,172,121,222,15,140,53,104,39,145,51,250,217, &
Si on applique le processus à l'ensemble des images, on en tire un fichier complet, qui semble être du code en Fortran. La compilation n'est malheureusement pas très probante.
$ gfortran sortie.f90 -o a.out
sortie.f90:57:16:
55 | DO I = 0,29,1
| 2
56 | ! - - - - - -
57 | DO I = 0,29,1
| 1
Erreur: La variable « i » à (1) ne peut pas être redéfinie à l'intérieur de la boucle commençant à (2)
sortie.f90:58:80:
58 | CHARACTER :: SSSS(0:255)
| 1
Erreur: Instruction déclaration de données inattendue à (1)
sortie.f90:59:80:
59 | INTEGER :: SSS(0:255)
|
... (une soixantaine de lignes d'erreur)
On se souvient de la précision dans l'énoncé (« sur les 79 cartes seules les 53 premières sont correctement numérotées »). Les 53 premières lignes correspondent en fait à des déclarations de variables, les 26 lignes restantes sont des opérations sur ces variables avec quelques boucles « for ». Après quelques essais, on arrive au résultat :
$ gfortran edit.f90 -o a.out
$ ./a.out
FCSC{#!F0RTR4N_1337_FOR3V3R!}
STOP 0
L'énoncé indique qu'on va nous présenter un circuit logique constitué uniquement de portes OU EXCLUSIF (XOR), avec 128 entrées et 256 sorties. On nous autorise à demander la sortie de 130 entrées différentes, puis c'est à nous de deviner quelle sera la sortie d'une entrée donnée. Si on y arrive, à nous le flag.
$ nc challenges.france-cybersecurity-challenge.fr 2302
===== Welcome to auBOOLot: Beat the Circuit! ======
[+] Please wait a bit during circuit generation ...
[+] Secret circuit generated! (26356 XOR gates)
Please provide a 128-bit binary input to evaluate:
>>> 00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Your output is 1001000110110100110000111111110101101110111100101000101111000001101010001010000011001101000111011010111010010011100001101110011100100000110001000110000111101110100010101111001010101001100010110111011010000011001111110111011011000001000011101100001000010000
Ici, on peut s'appuyer sur deux propriétés de l'opération XOR, notée ⊕. Dans la suite, A, B et C sont des variables booléennes valant indifféremment VRAI ou FAUX :
Dès lors, on peut schématiser le circuit logique en indiquant pour chaque sortie si oui ou non chacune des entrées intervient dans son calcul. Le circuit peut donc être modélisé par une matrice binaire 128×256, chaque ligne représentant une entrée et chaque colonne représentant une sortie.
Dernier détail, on remarque dans l'exemple plus haut que même lorsque toutes les entrées sont à 0 (FAUX), certaines sorties sont à 1 (VRAI). Or, on ne peut pas construire VRAI avec uniquement FAUX (car FAUX ⊕ FAUX = FAUX) (ce n'est pas de la philosophie, n'en tirez aucune leçon de vie). Cela signifie qu'il faut prendre en compte une sorte de 129e entrée valant tout le temps VRAI et intervenant dans le calcul de certaines sorties. Et ces sorties, se sont justement celles qui valent VRAI quand toutes les entrées sont à FAUX (vous me suivez ?).
On a donc notre première questions sur les 130 qui nous sont accordées. Pour celles qui suivent, on va « allumer » chaque entrée les unes après les autres, en gardant les autres « éteintes » :
Si vous voulez vous la péter, la énième entrée est égale à 1 << (128-n), où << est l'opération « décalage à gauche ».
Pour chaque sortie obtenue, on regarde si chacun des bits diffère de la sortie obtenue lorsqu'on a fourni une série de zéros. Si le bit est différent, alors le bit d'entrée valant VRAI intervient dans le calcul de ce bit de sortie.
À la fin, il nous reste une question qu'on peut se permettre de griller. Pour répondre au problème final, on a plus qu'à reprendre notre matrice patiemment constituée et calculer chaque bit de sortie. On prend comme valeur de départ la valeur du bit obtenu avec l'entrée nulle (000…000), puis on balaie la colonne de la matrice correspondant au bit de sortie qu'on souhaite calculer. Si la ligne vaut 0, alors on ne fait rien. Si la ligne vaut 1, on calcule OU EXCLUSIF avec le bit d'entrée correspondant.
Plusieurs problèmes de cette année prenaient pour appui un langage d'assemblage créé pour l'occasion (bien documenté, même si un peu abscons à première vue) et fonctionnant dans une machine virtuelle fournie. Pour chaque problème il fallait écrire un programme dans ce langage, ce qui n'était pas très compliqué mais exigeait un peu de concentration dès lors que le langage était très bas niveau.
Le premier problème, « Comparaison », est un problème d'introduction qui permet de prendre en main la machine virtuelle en effectuant une comparaison simple.
Le second problème, « Fibonacci », demande à calculer un certain terme de la suite de Fibonacci. Il faut jongler avec les différents registres pour stocker notamment le terme en train d'être calculé, le terme précédent et l'indice du terme. À la fin, on a un code qui ressemble à ça :
MOV R0, #0
MOV R1, #1
MOV R2, #0
MOV R3, #1
CMP R5, R2
JZR +5
ADD R1, R0, R1
SUB R0, R1, R0
SUB R5, R5, R3
JR -5
MOV R1, #0
STP
Si on compile le code et qu'on le fournit à la machine virtuelle :
$ python3
Python 3.10.9 (main, Dec 15 2022, 19:49:41) [GCC 12.2.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import assembly
>>> code = open("code.txt").read().strip().split("\n")
>>> assembly.assembly(code)
'800000008001000180020000800300010625c7054a414c084cedcffb800100001400'
>>> exit()
$ nc challenges.france-cybersecurity-challenge.fr 2301
Enter your bytecode in hexadecimal:
>>> 800000008001000180020000800300010625c7054a414c084cedcffb800100001400
[+] Congrats! Here is the flag: FCSC{770ac04f9f113284eeee2da655eba34af09a12dba789c19020f5fd4eff1b1907}
Une autre série de problèmes dans cette machine virtuelle appelle à reproduire l'algorithme RSA, un message et une clef étant fournis. La clef se constitue de plusieurs paramètres propres à RSA : les nombres premiers p et q, un exposant e, et d'autres variables issues d'opérations arithmétiques avec pleins de modulos :
e = 2 ** 16 + 1
dp = gmpy2.invert(e, p - 1)
dq = gmpy2.invert(e, q - 1)
iq = gmpy2.invert(q, p)
d = gmpy2.invert(e, (p - 1) * (q - 1))
Ce code utilise la bibliothèque gmpy2.
Si on applique l'algorithme rigoureusement, il faut calculer (m**d) % (p*q). Cela donne un résultat correct, mais ce n'est pas assez rapide pour résoudre le problème. Si on va voir à la source des spéficiations de RSA, dans la RFC 3447, section 5.2.1, on trouve la solution, moins directe, mais néanmoins bien documentée. Celle-ci se convertit assez facilement dans notre langage :
MOV R3, R8
MOV RC, RA
MOV RD, R7
POW R2, R5
MOV RC, R9
MOV RD, R6
POW R1, R5
SUB R4, R1, R2
MUL R4, R4, R3
MOD R4, R4
MOV R0, R7
MUL R0, R0, R4
ADD R0, R0, R2
STP
Ce qui permet d'obtenir le résultat :
$ python3
Python 3.10.9 (main, Dec 15 2022, 19:49:41) [GCC 12.2.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> import assembly
>>> code = open("code.txt").read().strip().split("\n")
>>> assembly.assembly(code)
'008300AC007D0352009C006D03514c8c4ee4024400704f004a801400'
>>> exit()
$ nc challenges.france-cybersecurity-challenge.fr 2352
Enter your bytecode in hexadecimal:
>>> 008300AC007D0352009C006D03514c8c4ee4024400704f004a801400
Which flag do you want to grab?
0. Quit.
1. Easy flag - check for code correctness and performances.
2. Medium flag - check resistance against several fault attacks, d not given.
3. Hard flag - check resistance against more fault attacks, not e and not d given.
>>> 1
[+] Testing correctness...
[+] Correct!
[+] Testing performances against the reference solution...
[*] Reference performances: 8972767.24 ns
[*] User performance: 6993844.04 ns
[*] Ratio: 0.78
[+] Congrats! Here is the easy flag: FCSC{06de1084d295f2a016f79485f2a47744bfb9ed3e30e9312121665559df9447de}
Voilà pour les problèmes de cette année ! Ils ne sont pas forcément bien représentatifs de la réalité de la cybersécurité, mais ont le mérite de faire travailler pleins de sujets techniques différents. J'ai le sentiment d'avoir plutôt appris des choses, notamment en rétro-ingénierie, ce qui est positif. J'ai aussi constaté la différence que cela faisait au moment d'aborder un problème quand on a déjà une culture technique du sujet, même minime. J'étais par exemple déjà familiarisé par avance sur le fonctionnement des cartes perforées, ce qui m'a permis de démarrer assez vite. Sur un autre problème, non expliqué ici et qui avait trait à la cryptographie sur courbes elliptiques, mes connaissances se limitaient à quelques vidéos YouTube, mais cela m'a quand même permis d'avoir une intuition du sujet et d'en tirer des résultats.
Sur ceux, merci de m'avoir lu. Je ne vous dis pas à l'année prochaine, j'espère qu'on se reverra d'ici là :^)
28 août 2022
Le choux romanesco est l'archétype de la fractale-dans-la-vraie-vie (source)
C'est en arpentant TikTok que je me suis pris d'un intérêt renouvelé pour les fractales. L'endroit est curieux, mais que voulez-vous, on y trouve de tout, et leur algorithme est si bon — à un point tel que c'en est inquiétant — qu'on finit toujours par tomber sur les niches correspondant à nos passions les plus tristes. J'étais sur TikTok donc, et une jeune femme entreprenait maladroitement de dessiner un triangle de Sierpiński en utilisant le jeu du chaos. Si les termes que je viens de citer vous échappent, nulle inquiétude, on va les prendre dans l'ordre.
Le triangle de Sierpiński est une figure usuellement obtenue comme suit :
Si vous répétez le processus suffisamment de fois (une infinité de fois en théorie, mais on risque de se heurter au mur de la réalité), vous allez aboutir à une figure nommée le triangle de Sierpiński :
Cette figure est une fractale, c'est à dire que si on agrandit une partie de la figure, on retrouve la figure entière. Par exemple ici, la moitié supérieure est une copie de la figure entière.
Si vous me permettez une incursion rapide dans les considérations mathématiques, cette propriété fait que les fractales n'appartiennent pas à une dimension entière, c'est-à-dire que ce ne sont ni complètement des lignes, ni des surfaces, ni des volumes. Elles ne sont pas exactement de dimension 1, 2 ou 3. Pour calculer leur dimension exacte, on peut faire l'analogie avec les figures classiques : si on multiplie la taille d'un cube par deux, son volume est multipliée par huit, soit deux à la puissance trois, car un cube est en dimension 3.
Pour trouver la dimension d'un triangle de Sierpiński, on peut noter que si on multiplie sa taille par deux, alors sa « surface » est multipliée par 3. Ainsi, sa dimension est égale à log(3)/log(2), soit environ 1,585. Le triangle de Sierpiński est donc environ à mi-chemin entre la ligne et la surface. Pour plus d'informations, voyez le concept de dimension de Hausdorff. Fin des calculs, retour à l'article.
Pour revenir à TikTok, je disais donc que la jeune femme avait opté pour une autre méthode, le jeu du chaos. Le processus est différent :
Ce processus a l'intérêt d'être assez ludique, aussi ai-je pris l'initiative de coder un script pour en simuler le fonctionnement. Rien de bien ambitieux pour l'heure, quelques lignes de Python qui génèrent une image au format SVG. Ce format texte a le bon goût d'être très facile à manipuler et se prête très bien aux images très géométriques avec lignes, points et polygones. Voyez comme c'est simple :
.jpg){kind=link}
<svg viewBox="0 0 1000 1000">
<rect width="100%" height="100%" fill="white"></rect>
<circle cx="66.98729810778065" cy="749.9999999999999" r="5"></circle>
<circle cx="933.0127018922192" cy="750.0000000000002" r="5"></circle>
<circle cx="500.00000000000034" cy="1.1368683772161603e-13" r="5"></circle>
<circle cx="487.55600750513696" cy="767.3399306075027" r="2" fill="red"></circle>
<circle cx="710.284354698678" cy="758.6699653037515" r="2"></circle>
<circle cx="388.6358264032293" cy="754.3349826518756" r="2"></circle>
<circle cx="660.8242641477243" cy="752.1674913259379" r="2"></circle>
<circle cx="796.9184830199717" cy="751.083745662969" r="2"></circle>
...
</svg>
Voici donc un triangle de Sierpiński produit avec cette méthode :
Cette figure comporte 50 000 points. On voit qu'on retrouve avec une précision surprenante le motif que nous avons déjà vu plus haut. À droite du sommet, on peut voir le premier point placé marqué en rouge, ainsi que sur le côté droit en dehors du triangle les points placés après, avant que le tracé ne vienne à l'intérieur du polygone pour ne plus en sortir.
Avec cet outil entre les mains, les multiples possibilités commencent à nous apparaître. En premier lieu, que se passe-t-il avec un autre polygone ? Ni une, ni deux, testons avec un carré. Ma déception fut perceptible.
C'est un carré du chaos.
Avec un carré, la répartition est donc parfaitement aléatoire. La science avance. En relisant l'article de Wikipédia en anglais sur le jeu du chaos, il est effectivement mentionné que « If the chaos game is run with a square, no fractal appears and the interior of the square fills evenly with points. However, if restrictions are placed on the choice of vertices, fractals will appear in the square ».
Par exemple, si dans notre carré on ne choisit pas à chaque tour parmi tous les sommets au hasard, mais on exclut du tirage au sort le sommet déjà choisi au tour précédent, on obtient la figure suivante, à l'esthétique bien plus intéressantes :
Il ne s'agit pas de la seule contrainte qu'on peut imposer dans la sélection du sommet. En fait, si à chaque tour on numérote les sommets dans le sens horaire à partir de zéro, zéro étant le sommet choisi au tour précédent, on peut coder une restriction en indiquant la liste des nombres parmi lesquels on peut choisir le prochain sommet. Ainsi, dans un carré, il y a quatorze « restrictions » possibles : (0) ; (0,1) ; (0,1,2) ; (0,1,2,3) ; (0,2) ; (0,2,3) ; (0,3) ; (1) ; (1,2) ; (1,2,3) ; (1,3) ; (2) ; (2,3) ; (3).
Dans cette liste, (0,1,2,3) et (1,2,3) sont les deux versions illustrées juste au-dessus. En effet, (0,1,2,3) correspond à l'ensemble des sommets du carré et dans (1,2,3) on a retiré le « 0 » correspondant par définition au sommet choisi au tour précédent. Si on essaie les versions (0,1,2) et (0,1,3), on a les résultats suivants :
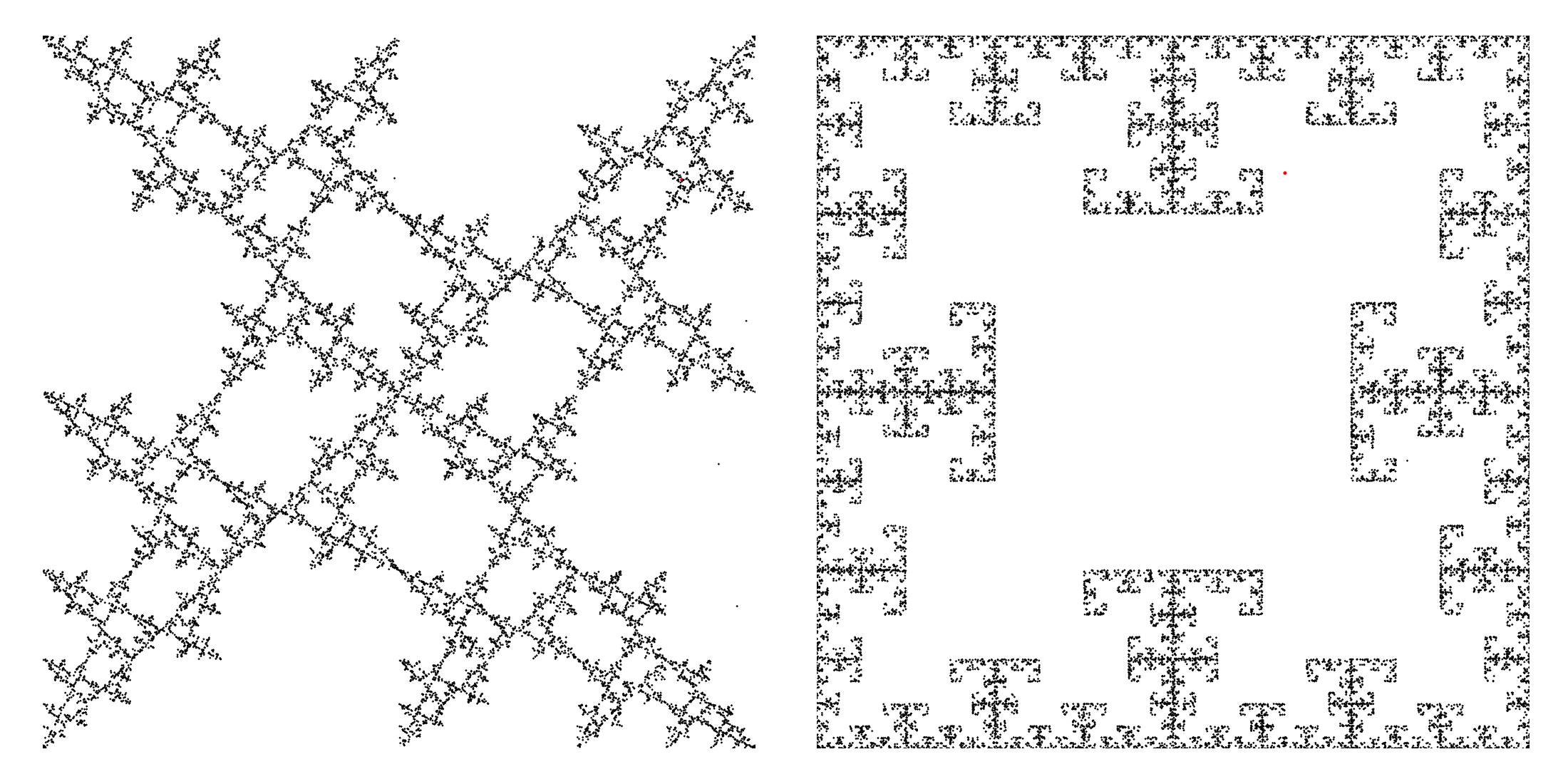C'est quand même plus rigolo que les nuages de points
On constate donc qu'on peut jouer sur deux facteurs : le nombre de côtés du polygone de départ et les contraintes sur le choix du sommet. Ces deux paramètres permettent la génération d'un grand nombre de figures variées, dont la plupart sont au moins aussi intéressantes que le triangle de Sierpiński d'où nous avons commencé notre voyage.
Si on s'intéresse aux pentagones, c'est encore un autre univers :
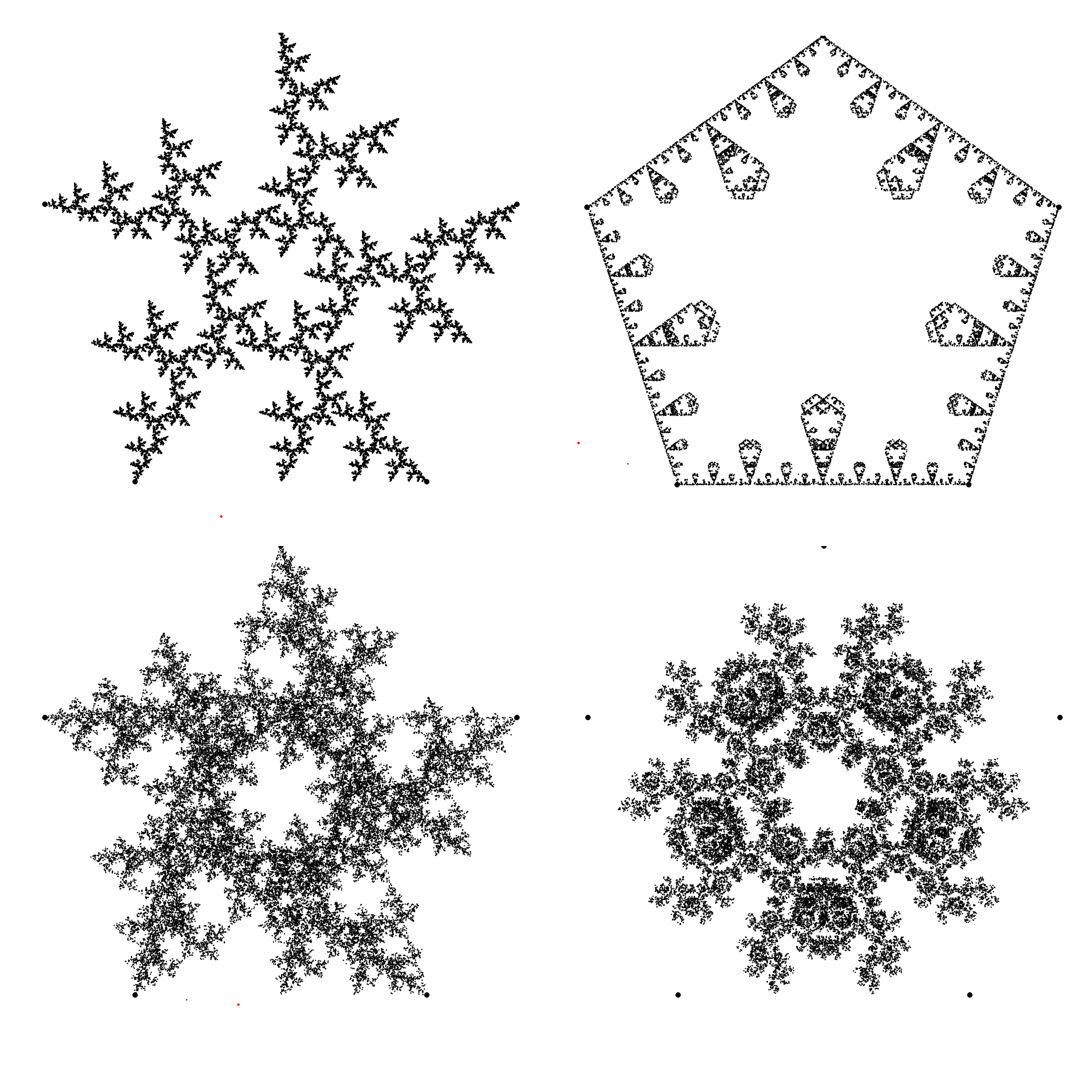Dans le sens de la lecture, nous avons (0,1,2) ; (0,1,4) ; (0,1,2,3) et (1,2,3,4), avec 50 000 points à chaque fois
En cherchant de nouvelles figures et avec ces nouvelles contraintes, le petit script Python du départ s'est avéré limité. Désireux d'avoir un outil pratique pour faire mumuse avec les jolis dessins, je me suis attelé à la conception d'une page web permettant de générer facilement les images. Le cahier des charges était de pouvoir renseigner un nombre de côtés, un nombre de points, une sélection de sommets, et d'en sortir une figure.
La transposition du Python au Javascript est aisée, mais je dois maintenant gérer un nombre quelconque de côtés. Pour trouver les coordonnées des sommets du polygone régulier, je ressors mes vieux souvenirs de classe préparatoire et les racines énièmes de l'unité. Un passage par le plan complexe plus tard, on trouve que si \(x_{0}\) et \(y_{0}\) sont les coordonées d'un sommet et \(n\) est le nombre de côtés du polygone, alors les coordonnées des sommets suivants seront :
$$x_{k+1} = x_{k}\cos\left(\frac{2\pi}{n}\right) - y_{k}\sin\left({\frac{2\pi}{n}}\right)$$
$$y_{k+1} = x_{k}\sin\left(\frac{2\pi}{n}\right) + y_{k}\cos\left({\frac{2\pi}{n}}\right)$$
La génération de l'image au format SVG ne pose pas plus de problème. Le défaut du SVG cependant est qu'il s'intègre tant à la page web qu'il est difficile de l'en sortir et de télécharger l'image produite. On ne peut pas en tout cas faire bêtement clic droit, « Enregistrer l'image sous… ». Je me suis donc lancé dans la tâche ardue de convertir le SVG en PNG, avant de reculer devant la tâche. J'ai fait un pas de côté pour générer un canvas. C'était finalement encore plus simple à manipuler que le SVG, et la conversion en PNG était facilitée.
Au bout du compte, vous pouvez à votre tour générer des images selon le jeu du chaos sur cette page. Le bagage scientifique me manque pour que je m'avance à qualifier de fractales toutes les images obtenues, on peut néanmoins au moins apprécier l'esthétisme graphique que nous offrent les mathématiques.
Panel de figures. Dans l'ordre de la lecture : heptagones (0,1,2) ; (0,1,3) ; (0,1,4) ; (0,1,5) ; (0,1,6) et hexagones (1,4,5) ; (2,4,5) ; (3,4,5)
Merci d'avoir lu jusqu'ici. Pour récompenser votre patience, voici la jeune femme de TikTok que j'évoquais plus tôt qui réussit enfin à tracer son triangle après avoir acquis une règle.